Tartalomjegyzék
*1. Bevezető
*2. Példák fraktál alakzatokra
*2.1 A Cantor sorozat
*2.2 A Koch görbe
*2.3 Sierpinski háromszög
*2.4 Mandelbrot halmaz
*2.5 Julia halmaz
*3. Fraktálok leírórendszere
*3.1 L-System
*3.2 IFS
*4. Fraktálok alkalmazása
*4.1 Fraktálok a természetben
*4.2 Fraktálok a gazdaságban
*4.3 Fraktálok a szociológia területén
*4.4 Fraktálok a művészetben
*4.5 Fraktálok a kép és hangfeldolgozásban
*4.6 Fraktálok és a jövő
*5. Fraktáltömörítési módszerek
*5.1 Másológép algoritmus
*5.1.1 A betömörítés elve
*5.1.2 Barnsley féle módszer
*5.1.3 Jacquin féle módszer
*5.1.4 Genetikus algoritmus
*5.1.6 A kitömörítés elve
*5.2 Fraktálkonverziós eljárás
*6. Egy fra
ktáltömörítő program megvalósítása *6.1 A program jellemzői
*6.2 A betömörítés menete
*6.3 A kitömörítés menete
*6.4 A tömörített file felépítése
*6.5 TGA file formátum
*6.6 Ötletek a program továbbfejlesztésére
*6.7 Felhasználói utasítások
*7. Összefoglalás
*SUMMARY
*8. Irodalomjegyzék
*
A szakdolgozat témáját a fraktálok illetve alkalmazási területeinek ismertetése képzi. A fraktálok világa egyre táguló, egyre több és több tudományág fedezi fel jelentőségét. Mivel meglehetősen új, érdekes és ismeretlen területtel állunk sze
mben, kihívásnak éreztem e témát feldolgozni.A káosz és a fraktálok a matematika egyazon ágába tartoznak. Mindkettőt a nemlineáris rendszerek tanulmányozása közben fedezték fel. Az elnevezést
Benoit B. Mandelbrot alkotta meg, aki elsőként foglalkozott fraktálgeometriával. Maga a szó a latin eredetű fractus kifejezésből származik, aminek jelentése: „törés”. A név arra utal, hogy törtdimenziójú alakzatokról van szó. Ez pedig azt jelenti, hogy le tud modellezni olyan alakzatokat, amelyek törtdimenzióval írhatóak körül. Jellemzőjük a nagyfokú önhasonlóság. Az alakzatok bármely részének nagyítása is hasonló alakzatokat eredményez, akármilyen mélységben is vizsgáljuk. A vizsgálatok szerint a káoszban megjelenő véletlenszerűnek tűnő geometriák a fraktálgeometria segítségével közelíthető. Könnyen modellezhető egy partszakasz, egy felhő, vagy akár egy fa növekedése. A modellezésen kívüli területeket a dolgozat 4. fejezetében ismertetem.A második fejezetben bemutatok néhány fraktáltípust, amelyek a számítógépes dem
ók kedvelőinek már ismerősek lehetnek. Ezt követően a fraktálok leírórendszereit veszem nagyító alá. Végül a lehetséges alkalmazások közül kiemelt fraktáltömörítéssel foglalkozok, amelyhez példaprogramot is készítettem.Számtalan féle alakzatban jelenhetnek meg fraktálok. Ezek közül a legismertebbekkel foglalkozok részletesen.
Egyszerű módon készíthetünk fraktálokat Cantor sorozat kialakításával. A sorozat kialakításának első lépése egy zárt intervallum [0,1] három egyenlő részre osztása. Az így keletkezett három rész közül a középsőt elhagyjuk. A másik két intervallumot pedig újra felosztjuk, majd ezt a műveletet folytatjuk tovább. Grafikusan ábrázolva a Cantor halmazt a 2.1-es ábrán látható képet kap
juk. Ennek megrajzolására alkalmas egyszerű algoritmus forráskódja a következő:Cantor(int x,int y,int ymeret)
{
if (ymeret>1)
{
rectangle(x,y,x+xmeret,y+ymeret);
recur(x+2*xmeret,y,ymeret/3);
recur(x+2*xmeret,y+2*(ymeret/3),ymeret/3);
}
}
A
Cantor rekurzív függvény egy bináris fa bejárási módszerével vázolja fel az alakzatot. Egészen addig a szintig rajzol, amíg a téglalapok magasságuk miatt már nem jeleníthetőek meg.

2.1 ábra: Cantor sorozat
Érdekes dolgot ta
pasztalhatunk, ha megvizsgáljuk annak a tartománynak a méretét, amelyet a kiemelt 1/3-ok méreteinek összesítésével érhetünk el, a végtelenségig végrehajtott műveletsor után.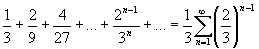
Ez pedig nem más, mint egy geometriai sorozat, amelynek értékét könnyedén kiszámíthatjuk:
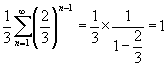
Azaz az eltávolított intervallumok mérete pontosan megegyezik a kiindulási mérettel. A sorozat a fraktálok azon jellemzőjét hordozza magán, hogy nagyítás esetén egyre több részlet jelenik meg, a felbo
ntás pedig finomodik.
A sokak által hópehelyként is ismert alakzat elkészítésének módja hasonlít a Cantor sor megrajzolásának módszeréhez. Az egyes szakaszok kivétele helyett azonban két újabbat helyezünk be, amelyek egy egyenlő oldalú h
áromszög oldalai lesznek. A megrajzolás lépéseit a 2.1-es ábrán láthatjuk.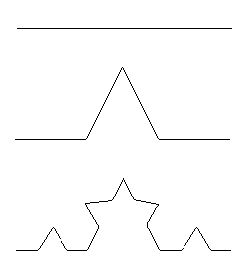
2.2 ábra: Koch görbe
A Sierpinski háromszög az egyik legérdekesebb és legkönnyebben megrajzolható
alakzat. Készítésének első lépéseként egy háromszög mindhárom oldalának felezőpontját összekötjük. Az így keletkező négy háromszög közül a középsőt kell eltávolítani.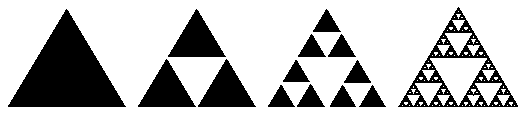
2.3 ábra: Sierpinski háromszög
A Sierpinski háromszöghö
z hasonló módszerrel rajzolható meg a Sierpinski szőnyeg. Ennek generálásához négyszögeket vagy köröket is használunk.
2.4 ábra: Sierpinski szőnyeg
A Mandelbrot és a Julia halmazok a komplex síkon megje
lenő objektumok. Ennek megfelelően leírásuk komplex számokkal végzett műveletek sorozataként adható meg. A végrehajtandó művelet:![]()
A z
egy olyan komplex szám, amely nulláról indul, és a halmazon belül - a műveletet rajta akárhányszor is elvégezve – nem éri el a végtelent. A C szám ugyancsak komplex mennyiség.Vegyük sorba az összes C
értéket a komplex számsík (-2 ; -1,25), (0,5 ; 1,25) téglalap által határolt területén, és mindegyik érték esetén addig végezzük a műveleteket, amíg az z értéke vagy a műveletek száma el nem ér egy adott számot! Ha a megadott számú műveleten belül nem érjük el a kijelölt z értéket, akkor a C pont a Mandelbrot halmazon belül van. Ha pedig ettől kevesebb iteráció elégséges, akkor ezen iterációk száma megadja a képpont színét. Az alábbi programrészlet segítségével rajzolhatunk ki egy Mandelbrot halmazt.int Iterate(float f,float fi)
{
float real=0,cplx=0,size,save=0;
int iterations=0;
do
{
save=real;
real=real*real-cplx*cplx+f;
cplx=2*save*cplx+fi;
size=real*real+cplx*cplx;
}
while ((size<100)&&(iterations++<100));
return (iterations);
}
for (i=1;i!=480;i++)
for (j=1;j!=640;j++)
putpixel(j,i,Iterate(-2.25+3.0*(j/640.0),-1.25+2.5*(i/480.0)));
A Mandelbrot halmaz szélén az egye
s részeket egymás után kinagyítva visszatérő, egymáshoz hasonló részeket – spirálokat, csápokat - fedezhetünk fel.
2.5 ábra: Mandelbrot halmaz
A Mandelbrot halmaz minden egyes C pontjához tartozik egy Julia halmaz. Ennek képét úgy kaphatjuk, hogy egy kiemelt C érték mellet z értékét pásztázzuk végig a komplex számsík egy területén. A pont színét itt is az iterációk száma adja. Ha a fenti Mandelbrot rajzoló algoritmusban néhány módosítást végzünk, alkalmassá válik Julia ábra rajzolására. Ebben az esetben f és fi értéke rögzítetté válik. A –0,75; 0,1 ponthoz tartozó Julia halmaz például igen szemléletes. Ezen kívül szükséges még kicserélnünk a szubrutinhívási paramétereket. Itt f, fi helyére a real és cplx változók kerülnek. Ha a programot futtatjuk, a 2.6 ábrán látható Julia halmazt kapjuk.

2.6 ábra: Julia halmaz
A fraktálok manuális és automatizált megjelenítéséhez, vizsgálatához definálnuk kell egy módsze
rt, amely egyértelmű utasításokat tartalmaz matematikai vagy grammatikai formában. Tudnunk kell, hogy általános módszer nincsen, nem használható bármelyik metódus bármelyik típusú fraktál megjelenítésére. Éppen ezért sokan ezek alapján csoportosítják a fraktálokat, az alábbi csoportokat képezve:
Az Aristrid Lindenmayer által 1968-ban kidolgozott módszer eredeti célja
a növényi fejlődés tanulmányozása volt. Az L-System (Lecture Notes Biomathematics) ezért alkalmas biológiai modellek felállítására. Segítségével könnyen leírhatunk egy teknőcgrafika lépéseit. Szimbólumai a toll mozgásirányának, lépései hosszának információit hordozzák.Lássunk egy példát az L-System alkalmazására! Mivel növények növekedésének modellezésére szolgált, a vizsgálat tárgya egy fraktál fa lesz. A rajzolás leírása a következő táblázatban összefoglalt elemek felhasználásával lehetséges.
|
F |
Előre mozgás |
|
+ |
Jobbra fordulás |
|
- |
Balra fordulás |
|
[] |
A belső műveletek elvégzése után visszatérés az eredeti pozícióba |
|
{} |
Extra hosszú vonal |
Legyen az elfordulások szögmértéke 20°, a kezdeti irány pedig 90°. Most pedig alkossuk meg a szabályt! Lépjünk a tol
![]()
A forma felhasználásával készült ábra egy Y-ra hasonlít. Ahhoz, hogy eredményül egy fára emlékeztető ábrát kapjunk, a forma összes
F szimbólumát helyettesítsük magával a formával. Az így kapott képlet:![]()
A műveletet sokszor egymás
után elvégezve a 3.1 ábrán látható képet kapjuk. Fraktál fa megjelenítésén kívül az L-System kiválóan alkalmas Koch görbe és Cantor sorozat leírására.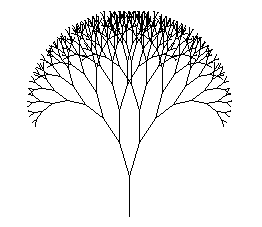
3.1 ábra: Fraktál fa
Az IFS kifejezés az Iterated System Functio
n szavak rövidítéséből származik. Sokkal több területen alkalmazható, mint az L-System. Használata a tömörítésben, modellezésben ugyanúgy elterjedt, mint a művészetekben. Lényege az, hogy egy alakzaton – halmazon – transzformációk sorát hajtjuk végre. Ez a művelet az un. affin transzformáció, amely egy lineáris transzformációból és egy transzlációból áll. Ezt az Euklideszi síkon a következő általános formában adhatjuk meg:![]()
Ez a kétdimenziós affin transzformáció mátrix formában is megadható:
![]()
Az A 2x2-es mátrix a lineáris transzformációt, míg a T
oszlopvektor a transzláció műveletét végzi. Az a, b, c, d, e és f konstansok különböző megválasztása különböző eredményekhez vezet, ám vannak olyan elemi affin transzformációk, amelyek segítségével bármilyen összetett transzformáció megvalósítható. Ezeket az 1. táblázatban foglaltam össze.Az alakzatokra (illetve azok pontjaira) alkalmazott affin transzformáció, amennyiben a konstansokat megfelelően választjuk meg, kontrakcióval jár. A sorozatban végrehajtott transzformációk hatására pedig az alakzat pontjainak koordinátái a tér egyetlen pontja felé kezdenek konvergálni. Ez az affin transzformáció fix pontja, amely véges méretű felbontás esetén fizikailag létezik,
látható. Másképpen az IFS attraktorának is nevezzük azt a halmazt vagy fix pontot, amelyhez a rendszer tart.|
Dilatáció |
|
|
Transzláció |
|
|
Tükrözés |
|
|
Forgatás |
|
|
Nyírás |
|
1. tábla: elemi transzformációk
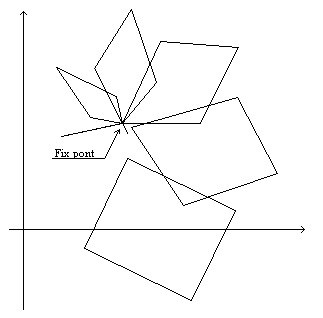
3.2 ábra: Kontrakciós leképzések és fix pontjuk
Az Iterált Függvény Rendszerek ilyen és ehhez
hasonló kontrakciós leképzések felhasználásával állítják elő a képet. Ez alapján, ha az IFS-t definícióval akarjuk meghatározni, a következőket mondhatjuk:Az IFS kontrakciós tulajdonságú affin transzformációk véges számú halmaza.
Két alkalmazását mutatom be. Az első az előző fejezetben már megismert Cantor sorozat, amelyet két transzformáció segítségével írhatjuk le:
![]() ,
,
![]() .
.
Itt w1 és w2 is kontrakciós leképzés. Az attraktor maga a Cantor halmazbeli elemek összessége. Ha az IFS-t egy harmadik (![]()
A másik, jól ismert alkalmazása az iterált függvény rendszereknek a Sierpinski hár
omszög. Ez az alábbi három affin transzformáció sorozataként állítható elő: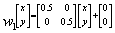
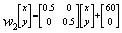
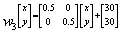
Egyetlen mátrix felírásával általános formában is leírhatjuk a háromszöget. Ekkor egy táblázatban foglaljuk össze a konstansokat. A táblázat a 2. ábrán látható.
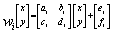
|
w |
a |
b |
c |
d |
i |
f |
|
1 |
0.5 |
0 |
0 |
0.5 |
0 |
0 |
|
2 |
0.5 |
0 |
0 |
0.5 |
60 |
0 |
|
3 |
0.5 |
0 |
0 |
0.5 |
30 |
30 |
2. tábla: Sierpinski háromszög IFS mátrixának kódjai
Kétféle módszer kínálkozik arra, hogy az IFS segítségével fraktálokat készíthessünk. Az egyik, a véletlen iterációs algoritmus. Ennek lényege, hogy a kép egy területén kijelölt pontot a képen belülre affin transzformációval képzett kis
ebb méretű kép megfelelő részére illesztjük. A megfelelőségen itt a transzformáció által meghatározott pontot értjük. Belső képből annyi létezik, amennyi leképzési szabályt alkalmazunk az alakzatra. A Sierpinski háromszög esetén például háromból épül fel. Ezek közül véletlenszerűen választunk ki egyet. A véletlenszerűség befolyásoló tényezője egy számérték, amely mindegyik transzformációra egyenként meg van adva. Ismét a Sierpinski háromszöget véve példaként, a valószínűség mindháromnál azonos, 1/3-val egyenlő. Az első pontbehelyezés után a következő transzformált képbe kell a pontot tenni, annak megfelelően, hogy az eredeti képben hol helyezkedik az első transzformáció során kirajzolt pont. Ezt a műveletet kell elvégeznünk újra és újra.A másik módszert det
ermisztikus metódusnak hívják. Ezt használva sokkal több memóriára és időre lesz szükségünk. Működésének mechanizmusa teljes képek másolásából áll. Ezt a módszert példán keresztül részletesebben is ismertetem.Legyen a kiindulási képünk egy papagáj fekete
-fehér nyomdai fotója és legyen három transzformációnk. Az előbbi a 3.3 (b) ábrán, az utóbbiból létrehozott három keret az (a)-n szerepel. Első feladatunk, hogy a három kis keretbe transzformáció segítségével behelyezzük a papagáj képét. Ez után, az így létrejött (c) képet mentsük el. Most (a) mindhárom keretébe rakjuk be az elmentett képet. Ezt a műveletet folytassuk, amíg két egymás után elkészült kép között már nem látunk különbséget. Ebből az tűnik ki, hogy véges számú iteráció elvégzése után a felbontástól függően a kép már nem változik. Ez a transzformáció fix képe, a három affin transzformáció attraktora, az azok által létrehozott fraktál (g és h ábra). Ha megvizsgálnánk még egy ábrát, mondjuk egy szekrény képét, azt látnánk, hogy az iterációk végrehajtása után teljesen ugyanahhoz a fraktálhoz jutunk. Tehát a fraktál független a kiindulási képtől.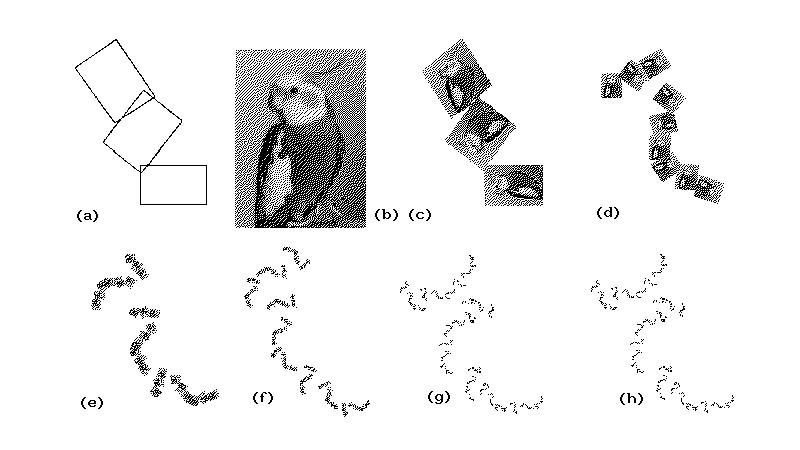
3.3 ábra: IFS fraktál determisztikus módszerrel
Nem esett szó arról, hogy mi történik abban az esetben, ha a transzformációk á
ltal létrehozott keretek, képek fedik egymást. Ha egy bit színmélységgel dolgozunk, akkor a háttértől elütő szín a meghatározó. Amennyiben két vagy több keret közül akár egyik is ilyenre színezi, a többi már nem módosítja.Mi azonban a feladat, ha nem egy
bites a színmélység, ha több szürkeárnyalat van, netán színes a kép? Szürkeárnyalatok esetén a közös pont intenzitására minden azt érintő keret befolyásolólag hat. A véletlen iterációs módszernél említett véletlen érték tulajdonság itt is szerephez jut. Ez, mint egy szűrőtényező viselkedik. Mindegyik affin transzformáció csak ezen értékének arányában módosítja a közös pontot. Ugyanez az elv érvényes a színes képekre is, ahol akár az RGB akár a YUV összetevőket egyenként összegezhetjük.A fraktálok az élet sok területén jutottak már eddig is szerephez, azonban a felhasználások köre bővülőben van. Néhány olyan területet emelek ki amelyeken sikerrel használják az elméletet.
Ma már bizonyított, hogy a t
ermészet kedveli a fraktálalakzatokat. Átszűrődési (perkolációs) fürtöknek nevezett fraktálokat ismertek fel például a szilárd szemcsézetű anyagokban átáramló folyadékok (így a talajban szivárgó víz vagy az őrölt babkávé szemcséi között átszűrődő feketekávé) mintázatában. A korom, a kolloidok és egyes polimerek szintén fraktáloknak tűnnek. Ugyancsak fraktálok jelennek meg légbuborékok olajban történő mozgásakor, bizonyos kristályok növekedésekor, vagy a villámcsapásokra emlékeztető elektromos kisülésekben. A felhők szabálytalan mintázata és a tengerpartok csipkézettsége is szinte bizonyosan fraktálnak tekinthető. A természeti fraktálok létezésére vonatkozó bizonyítékok gyarapodtával a kutatók vizsgálni kezdték a fraktálok kialakulásának kérdését. 1981-ben Thomas A Witten III (Exon Research and Engineering Company) közreműködésével a gödöllői FM műszaki intézet kidolgozott egy fraktálnövekedési folyamatot, és azt diffúzió által szabályozott felhalmozódásnak (diffusion-limited aggregation,vagy röviden DLA) nevezte el. A modell szerint egy bizonyos fajta rendezetlen és megfordíthatatlan növekedési folyamat egy különleges fraktáltípust eredményezhet. Az elmélet abból a szempontból is vonzó, hogy fogalmilag egyszerű és számítógéppel könnyen modellezhető.A DLA-mode
ll jelentősége abban áll, hogy rámutat a fraktálok és a növekedés közötti kapcsolatra. A természeti tárgyak sokféleképpen növekedhetnek. Egy ideális kristály például az egyensúlyi állapot közelében növekszik: sokféle elrendeződést "kipróbál", míg csak rá nem talál a legstabilabb szerkezetűre. Amikor egy növekvő kristályhoz egy újabb molekula kötődik, általában csak egy sor lehetőség végigvizsgálása után kapcsolódik az arra alkalmas helyre; az egyensúlyi kristály lassan és állandó átrendeződések közepette alakul ki. A legtöbb valódi növekedési folyamat azonban nem rendelkezik ennyi idővel. Az élet például, bármely formáját nézzük is, nem egyensúlyi folyamat. A fraktálok nagy részének növekedése ugyancsak az egyensúlytól távoli.Képzeljük el, hogy egy részecs
ke fürt a következőképpen növekszik: ha időről időre egy-egy részecske hozzáér a növekvő képződményekhez, egyszerűen odatapad, anélkül, hogy más helyekkel próbálkozna. Az ilyen folyamatot nevezzük halmozódásnak. A halmozódás a nem-egyensúlyi folyamatok szélsőséges esete, mivel egyáltalán nem megy végbe átrendeződés. Tegyük fel, hogy a részecskék véletlenszerű bolyongással jutnak el a fürt közelébe: az egymást követő lépések nagysága és iránya véletlenszerű. A részecskéknek ezt a véletlenszerű bolyongással történő felhalmozódását nevezik DLA-nak, amelynek tárgyalása túlmutat a szakdolgozat keretein.
Guastello S.J. 1995-ben kiadott művében, a
Chaos, catastrophe and human affairs: Applications of nonlinear dynamics to work, organizations, and social evolution (Káosz, katasztrófa és emberi ügyek: A nemlineáris dinamika alkalmazásai a munkában, szervezetekben és szociális fejlődésben) számtalan modellt állít fel élő rendszerek struktúráinak vizsgálata céljából, azzal a nem titkolt céllal, hogy jövőjükre vonatkozóan is jóslásokba bocsátkozhasson. Az egyik gyakorlati témájában a káosz attraktorainak szerepét például a munkanélküliségi mutató változásában is bizonyítani próbálta.A közgazdaságtanban megállapított egy minimális munkanél
küliségi érték, amely rövidtávon az infláció (és ebből kifolyólag a banki kamatok) által szabályozható, illetve viszont. Ezen érték szerint a munkanélküliség stabilis értéke 6,7% körül mozog. Statisztikai adatokat felhasználva Guastello nemlineáris rendszere a 6,6% felé konvergált. Ellenőrzésképpen a transzformációkat visszafelé is elvégezve visszakapta a statisztika első számadatát, a kiinduló feltételt. Sikerült hát olyan modellt felállítania, amely alkalmas egy statisztikailag hosszútávon stabilizálódó gazdasági mutató számítására.A modellbe ezután különböző sokkoló tényezőket vitt, szélsőséges paraméterváltozásokat okozva. Számtalan iteráció után a rendszer ismét az előző százalékhoz konvergált, habár attól egy szinttel magasabb értéken stabilizálódott. Az állami beavatkozást (monetáris politikai elemeket) szimuláló, szűkülő paraméterrendszer hatására a konvergencia gyorsult, de hosszútávon nélkülözhetőnek bizonyult.
4.3 Fraktálok a szociológia területén
A szociológia területén járatosak számára ismert lehet a Divergencia Szindróma, amely szerint létezik egy tendencia, egy törekvés azokban, akik a szociális rendszereket, szervezeteket felállítják, egy stabil állapotra, amely az élet természetes folyamát konzerválja.
Érdekes különbséget képezni emberek ösztönös, érzelmi és megfontolt, mérlegelt válaszai között, amikor egy szociális helyzetet változtató “furcsa attraktor” hurkába kerülnek. Természetesen az embe
rekre inkább az előbbi jellemző, a változások által hozott kényelmetlenségre dühvel, a rizikóra félelemmel reagálnak, megpróbálván ellenállni. A legtöbb ember érzelmekkel reagálva nem képes (vagy nem is akarja) látni a kreatív lehetőségeit vagy hosszútávú előnyeit annak a fraktál fejlődésnek amely ifjúkorában nem hoz mást csak kényelmetlenségeket. Az önszervező szociális rendszerek mindig megadják magukat az érzelmileg vonzó stabilitásnak, ami egy vulkán kupakja, és ami jól működik a katasztrófa pillanatáig.Ezért egy jól működő rendszer nyitott a kritikákra, és ha nem is próbálja irányítás alá vonni a Divergencia által előidézett változásokat, azokat megérti és gyorsítja. A Complexity International magazin által felhozott példák között szerepelt az Európai Unió mintájára létrehozandó orosz, belorúz, kazakhsztán és kirgisztán szövetség, amely az orosz elnök tanácsára Bulgáriával is kibővülhetett volna, ám a bulgár lakosság tiltakozásával találkozott. A változás elutasítása miatt tombol jelenleg is a Balkáno
n háború.Nehéz megmondani, hogy egy szociális rendszer hova konvergál, ám folyamatos iterációja a rendszer fejlődését biztosítja.
A művész, aki saját magát “fraktalista”-nak hívja, meglepően sokat örököl a művészet történetéből. Számtalan művész alkalmazta ugyanis a technikát, még ha nem is ismerte definicióját, matematikai hátterét. Olyan neveket érdemes itt megemlíteni, mint például Vincent Van Gogh, aki energia sűrű örvényeibe burkolta tárgyait, vagy akár Escher rekurzív
geometriái. Az építészetben kiemelkedő alkotásnak számítanak a Párizsi Operaház részletes barokk díszítései, vagy a gótikus katedrálisok ismétlődő ívei.A huszadik század végén azonban már öntudatos a fraktalizálás. A művészet egy önmagára utaló, önmagát reprodukáló rendszerré vált, amelyben a művészek élvezettel ismerik fel a fraktalizálás művészeti jellegét.
Azonban felmerült egy nagy kérdés: olyan területet közelítünk-e meg, ahol egy számítógép helyettesítheti a művész intuicióját? Amíg a válasz nemleges, az önhasonlóság fraktál mértékei, a párhuzamos sorrendiség és a káosz úgy tűnik, segít – egy - a művészet természetben fontos dolog megvilágításában.
Vegyük a véletlenül képződő önhasonlító fraktálokat (mint amilyenek a fák és a hegyek) és a számítógép által generált nemlineáris fraktálokat (például a Mandelbrot halmazt), ahol a minták különböző méretekben ismétlődnek. Ha a Mandelbrot halmaz azon spirális, érdekes formáit tekintjük, amelyek a halmaz végtelen partvonala körül örvénylenek, hamarosan kis
zámíthatónak tartjuk őket. Természetesen ez a kiszámíthatóság inkább pszichológiai okokra vezethető vissza. Egy idő után e tájak szemlélése unalmassá válik.Ha a Mandelbrot halmazt egy igazi műalkotással hasonlítjuk össze, mint amilyen Picasso képe, vagy akár Shakespeare műve, rájöhetünk, hogy az utóbbiak legyenek akármelyik periódus, stílus vagy kultúra munkái, megőrzik vitalitásukat szemünkben, akárhányszor is találkozunk velük. A nagyszerű költemény, festmény mindig új élményt nyújt. Mona Lisa mosolya p
éldául örök talány marad.
4.1 ábra: Nachume Miller festménye
Tudományosan megvizsgálva a jelenséget arra a következtetésre juthatunk, hogy a maradandó műalkotás valamilyen módon ellenáll agy azon késztetésének, ami a megszokás tartományába taszítaná. Úgy tűnik, hogy egy nagyszerű munka mindig újabb “furcsa attraktort” prezentál. Ez az attraktor a művész képzelete és keze által születik, és ez a kulcsa művek élvezetének.
Természetesen a fraktálművészet nem csak festészetből, építészetből és szobrászatból áll, a fraktálok hatást gyakorolnak a zenére is. A fraktálzene teória az úgynevezett “rózsaszín zajon” alapul. Tapasztalatok szerint ez sokkal kellemesebb a fülnek, mint a fehér vagy barna zajok, amelyek közül az első túl vél
etlenszerű a második pedig túlzottan merev. Mandelbrot tanulmánya alapján az idegrendszer perifériájának zaja fehér típusú, de az agy belső felé haladva rózsaszínűvé válik.A fraktálzene a zaj hullámképének vonalábráját felhelyezi egy kottára, és hangjegyeket rendel annak pontjaihoz. A hangok hosszát ugyancsak a zaj határozza meg, egy második hozzárendelés segítségével.
4.5 Fraktálok a kép és hangfeldolgozásban
A fraktálokat alkalmazzák a kép és hangfeldolgozás területén is. Egyrészt felismerésre kiválóa
n alkalmas, hiszen a felismerendő hang vagy kép fraktálokra való felbontás után egy matematikai képletben leírható, így képletek paramétereinek összehasonlítására redukálódik le a feladat. Használható az elmélet tömörítésre is, hiszen a képletek paraméterei valószínűleg kevesebb helyet foglalnak el, mint maguk a nyers adatok. Természetesen mindegyik alkalmazásnak komoly matematikai háttere van. Algoritmusok ugyan léteznek de sok közülük egyenlőre nem automatizálható.A szakdolgozat kiemelten foglalkozik a
témán belül az állóképek tömörítésével. A legjobb fraktál alapú képtömörítő programok azonos hűség mellett kisebb méretet érnek el, mint a jelenleg legjobb tömörítési arányúnak tekintett JPEG. Hatalmas a különbség nagy hatásfokú (kis hűségű) tömörítés esetén, amikor a fraktál file a JPEG file akár tized része is lehet.A képtömörítés területén már látszik némi szabványosságra való törekvés, elkészült a FIF formátum, amelyet néhány internetes böngészőprogram is ismer. Nem véletlenül jelenik meg éppen e területen a fraktál technológia. A sávszélesség korlátozásának feloldása ugyanis sokkal nehezebb feladatnak tűnik, mint matematikai teljesítményükben kiemelkedő számítógépek tervezése és gyártása.
Távlati lehetőségek kiaknázhatatlan
tárházát képzik a fraktálok. Ezek közül csak néhány példát említenék:
5. Fraktáltömörítési módszerek
A fraktálok számítástechnikával kapcsolatos egyik legfontosabb alkalmazási területe a képtömörítés. A fraktáltömörítő eljárásokat alapvetően két csoportba oszthatjuk. Az elsőbe azok tartoznak, amelyek a kiindulási képből vett nagyobb részletekhez hasonlítják a kép kisebb részleteit. A másik csoportot egy fraktálkönyvtárból szabadon válogató összehasonlító képzi. Az alapelvek mindkét csoportnál hasonlóak.
A másológép algoritmus gyakorlatilag nem használ fraktálokat a tömörítéshez, azonban az alkalmazott transzformációk és a folyamatos iterálás miatt szokás fraktáltömörítőnek tekinteni.
Elsõ lépésben a tömörí
tendő képet, felületét teljes mértékben lefedõ, adott méretű négyzetekre, úgynevezett domain blokkokra kell felbontani. A domain blokkok ideális mérete függ a teljes kép méretétől, illetve attól, hogy milyen minőségben és mekkora számításra szánt idővel szeretnénk reprodukálni. Az ajánlások szerint használhatunk 4x4, 8x8, 16x16 vagy akár 32x32-es blokkokat is. A kis méretű domain blokkok használatának előnyei közé tartozik, hogy geometriailag könnyen elemezhetőek, osztályozhatóak, gyorsan hasonlíthatóak és pontosabb tömörítést tesznek lehetővé. A 8x8 és nagyobb domain blokkokat az egyenletes képi területek redundanciájának jobb kihasználása és nagyobb tömörítési arány jellemzi.A következő lépés a kép domain blokkoknál nagyobb területű, range blokkokra való felosztása. A range blokk mérete általában kétszerese domain blokkénak. A range blokkokat ezek után negyedére zsugorítjuk, amivel eléri a domain blokk méretét. A kicsinyített domain blokkokról másolatokat készítünk, és rajtuk olyan különböző transzformá
ciókat végzünk, mint a forgatás, tükrözés és az árnyalatok, fényességi értékek megváltoztatása.Ezután minden domain blokkhoz meghatározzuk a hozzá legjobban hasonlító zsugorított range blokkot. A kiválasztott blokk koordinátáit és a rajta alkalmazott trans
zformáció típusát, együtthatóit mentjük el a tömörített állományba. Az állományban megjelenő adatok összessége pedig az IFS kódja.Felmerül a kérdés, hogy hogyan hasonlítjuk össze a blokkokat. Ennek egyik módszere az RMS (Root Mean Square) számítás. A ké
t blokk pontjai különbségének négyzeteit összegezzük, és ebből vonunk gyököt. Minél kisebb az érték annál jobban hasonlítanak egymásra. Ennek képlete az alábbi: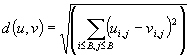
A képletben szereplő
B a domain blokk mérete, u és v a két kép pontjainak fényesség értéke, illetve színes képek esetén valamelyik összetevő intenzitása.Tudnunk kell, hogy nem feltétlenül kell minden domain blokkot minden range blokkal összehasonlítani. Hogy csökkenjen a számításigény (különösen a domain blokkokhoz képest nagy képek esetén) ez által gyorsabbá váljon a tömörítés, többféle keresési metódust dolgoztak ki a témával foglalkozó tudósok. Példaként álljon itt három módszer bemutatása.
Barnsley alapvető algoritmusa még nem osztotta fel a képet range blokkokra, helyette az egész képből képzet fraktálokkal (mint a 3. fejezetben bemutatott papagáj) hasonlította össze a kép részleteit. Nem szigorú domain blokk felosztásra kell gondolnunk, inkább szabad szemmel is látható hasonlóságokra. Ba
rnsley átfedésekkel is dolgozó IFS-t használt. Ezek miatt a folyamatot nem lehetett automatizált algoritmussal megoldani.Arnaud Jacquin Barnsley tanítványaként rájött arra, hogy egy képnek nem az egész képből felépülő fraktálokból kell állnia. Vizsgálatai rámutattak arra, hogy jobb eredmény érhető el, ha a kép több darabját használjuk fel. Tőle származik tehát a fent ismertetett módszer elméleti alapja. Az alapvető algoritmus, amely minden domain blokkot minden range blokkal öss
zehasonlít az alábbi módon épül fel:for (minden domain blokkra)
d = végtelen
for (minden range blokkra)
for (minden transzformált blokkra)
di = hasonlósági fok
ha (di < d) d = di , w = wi
w mentése
Jacquin a kétszintű, 8×8 és 4×4-es, blokkok használatát javasolja. Kétszínű blokkok esetén könnyen végezhetünk csoportosítást élek, középértékek és intenzitások tekintetében. Ezzel drasztikusan csökkenthetjük az összehasonlítások számát.
Nem válik gyorsabbá, ám lényegesen jobb reprodukált képet eredményez a genetikus algoritmus használata.
A genetikus algoritmus alkalmazása a következő lépésekből áll:
Az algoritmus komponensei pedig:
Az első lépésben, az inicializálás során készítjük el az első populációt, amelynek elemei olyan sztringek amelyek megoldások lehetnek a kijelölt feladatra. A biológiai hasonlóság miatt kromoszómáknak is hívhatjuk ezen sztringeket.
A populáció összes egyedét megvizsgáljuk, és az azok közül legal
kalmasabbakat választjuk ki reprodukálásra. Az új elemeket úgy kapjuk, hogy a kiválasztott egyedekre alkalmazzuk az operátorokat. Két egyed szükséges a párosítás operátorhoz, amely a kettő különbségéből képez új elemet. A mutációs operátor viszont egy elem bizonyos részeinek, jellemzőinek módosítására alkalmazható.A maradék – reprodukálásra alkalmatlan – egyedet pedig kicseréljük az újakkal. Ezzel újabb generációt hoztunk létre, amely ha nem alkalmas a feladat kijelölt közelítési szintű megoldására, új rep
rodukálásra szorul, azaz az algoritmust tovább kell folytatnunk.Maga az algoritmus tehát a potenciális válaszok populációjának generációit fogja iterálni, minden szintnél kiválasztva az alkalmas egyedeket és felhasználva őket új egyedek létrehozására a genetikus operátorok segítségével. A problémát itt az alkalmas egyed kiválasztása jelenti. A biológiai természetes szelekcióhoz hű szimuláció mindig a “legfittebb” egyedet produkálja újra, amelynek felismeréséhez valamiféle mértékre van szükségünk. A mérés
elvégzésére szolgáló függvényben felhasználhatnánk a Hutchinson metrikát (Barnsley 1988-as publikációja), de ez több ok miatt sem igazán alkalmas automatizált, számítógépes feldolgozáshoz. E helyett inkább apró részletekre bontjuk a generáció elemeit, és a négyzet alakú részletekben szereplő pontok számát hasonlítjuk össze, majd ezeket a különbség értékeket összegezzük. A populációban ideális fittséggel rendelkező egyed fittségi mérőszáma magasabb, az egyhez közelít. Az általános kiválasztási szabály pedig:f(i)/[f(1) + ... + f(n)]
A genetikus algoritmus első gyakorlati megvalósításánál fény derült arra, hogy a mutációs operátorok igen kis szerepet játszanak az új generációs egyedek elkészítésében.
A fraktáltömörítésben, a gyakorlati megvalósítás során a populáció egyedei nem mások, mint helyi IFS transzformációk, amelyeknek mutációi és párosításai hatására az általuk létrehozott transzformált range blokkok (attraktorok) egyre nagyobb hasonlóságot mutatnak a kép részleteihez (domain blokkok).
A tömörített állományban eltárolt adatokból a képet többszöri iterá
cióval nyerhetjük vissza. Először két - a kép méretének megfelelő - memóriatömböt kell lefoglalnunk. Az egyik a domain, a másik pedig a range blokkok tárolásához szükséges. Ezeket először felosztjuk a megfelelő méretű területekre, majd a range blokk memória területére egy tetszőleges képet helyezünk.Az állományból kiolvasott információk alapján a range blokkokat transzformálva, kontrakciónak alávetve a másik képen található megfelelő domain blokkok helyére másoljuk. A másolások elvégzése után keletkezett képet átrakjuk a range blokk memória területre, majd újra kezdjük a másolási folyamatot. Az algoritmus kilépési feltételei a következők lehetnek:
Ha nem az eredeti képből IFS segítségével készült fraktálok, vagy helyi IFS transzformációkkal leképzett apróbb képrészletekből akarjuk összeállítani az eredeti képet, akkor használhatunk olyan fraktálokat, amelyeket képletek segítségével írhatunk le. A fraktálokat különböző típusokból válogatjuk össze. Ezek között szerepelhet akár egy Mandelbrot halmaz bármely kinagyított részlete, akár egy transzformált Koch görbe.
A tömörítést itt is a kép felosztásával kezdődjük, ám nem feltétlenül azonos, egymás mellett helyet foglaló részleteket veszünk. Okosabb módon kell a képet áttekintenünk, és akár egymást is lefedő domain blokkokat képeznünk. Megtehetjük azt is, hogy akár az egész képet tekintjük részletnek, és a későbbiekben bontjuk tová
bbi darabokra.A fraktálokat egy listába foglaljuk, majd ezek közül választjuk ki azt, amelyik a legjobban hasonlít az adott képrészletre. Ezután addig változtatjuk a fraktál paramétereit, amíg el nem érjük a megfelelően hasonló képet. A kimeneti állományba
csak a fraktál típusa és annak paraméterei kerülnek.A fraktálkonverziós eljárás inkább fekete-fehér, illetve szürkeskálás kép tömörítésére alkalmas. Tömörítési aránya lényegesen jobb lehet, mint ami a másológép algoritmussal elérhető, ám a betömörítésre szánt idő nagyságrendekkel több.
6. Egy fraktáltömörítő program megvalósítása
A szakdolgozat előző fejezeteiben ismertettem a fraktálok készítéséhez, illetve képek fraktáltömörítéséhez szükséges alapvető matematikát, módszereket. Ebben a részben az általam készített fraktáltömörítő program gyakorlati megfontolásait és működését írom le.
A szoftver Windows 95 operációs rendszert, vagy Win32 környezetet igényel. A választott programnyelv a Borland C++ 4.5, melyben az ObjectWind
ows támogatás és a Win32-es környezet megfelelő lehetőségeket biztosít egy ehhez hasonló alkalmazás elkészítéséhez. A program 8 bit mélységű szürkeárnyalatú TGA formátumú képek nagy hatásfokú be- és kitömörítésére alkalmas. Szabályozható a kitömörítés minőségi tényezője.A program projektként tölthető be az IDE-be. A projekt központi állománya a
compfrac.cpp amely a főablak menürendszerét kezeli. A be- és kitömörítést segítő közös rutinok a fractal.h állományban helyezkednek el, míg a comp.h és a decomp.h állományok csak a nevükből is következő egy-egy funkciót tartalmazzák.
Az állományok kiválasztása után hívjuk meg a compress
függvényt. A függvényben először beállítjuk a zsugorított range és domain blokkok méreteit. Ezek jelenleg kötötten 4x4-esek, de az összehasonlító és átlagoló rutinok átírásával könnyen megvalósítható egy nagyobb blokkméret is. Mind a domain, mind a range blokkok, sőt a kép leírását is egy-egy struktúra hordozza (pictureblock). Ennek eleme az előbb beállított x és y méret, a pixelekben kifejezett hossz és egy mutató ami az első képpontra mutat abban a bufferben amit dinamikusan foglalunk – a következő lépésben.A be- és kimeneti állományok megnyitása után beolvassuk a TGA fejlécet, és a kép adatait. Ez után
a kép leátlagolása történik, minden egyes range blokkot felére redukálunk, egyszerű átlagszámítással. Gyakorlati megfontolások alapján a kép intenzitását is módosítjuk, minden pont fényességét ¾-ére csökkentjük.Mivel a betömörítési idő nagyon hosszú, egy nem modális ablakot nyitunk, amelybe folyamatosan kiírt százalékértékek tájékoztatást adnak a tömörítés állapotáról. A számítások végzése alatt az ablakobjektumok egyetlen eseménymetódusa sem érhető el, ezért a rendszer “nem felel” státuszt jelezhet. Ez
en ok miatt is szükség van egy hasonló megoldásra, ami tájékoztatást ad arról, hogy a program nem “fagyott le”.Indulhat a blokkok összehasonlítása. Végigmegyünk az összes domain blokkon, azaz a külső ciklus sorról sorra halad végig a képen. A gyakorlat azt bizonyította, hogy nem okoz problémát, ha a sorok végén és elején a domain blokkok esetleg átlapolódnak. Ez abban az esetben fordul elő, ha a kép természetes szélessége nem osztható a domain blokk szélességével, ami jelen esetben négyet jelent.
Az aktu
ális domain blokkot bemásoljuk egy erre a célra elkőkészített bufferbe, majd kiszámoljuk pontjainak egyszerű intenzitás átlagértékét. A belső ciklus ugyanezt teszi egyenként az összes zsugorított range blokkal. A range blokk intenzitásának mértékét kivonjuk az aktuális domain blokk átlagából, és az eredményt arra használjuk fel, hogy módosítsuk a range blokk intenzitását. Ezek után elkezdjük elvégezni a kijelölt transzformációkat. A programban a range blokkot nyolcféle műveletnek vetjük alá (flip). A műveletet leíró szám három alsó bitje fontos, ezek képviselnek egy-egy transzformációt, úgy mint x, y irányú tengelyre valamint az átlókra való tükrözést.Minden egyes transzformáció után megvizsgáljuk, hogy mennyire tér el az átalakított range blokk a domain blokktól. A differenciát vizsgáló (difference
) függvény a pontok különbségének négyzetösszegét képzi, és ezzel tér vissza. Amennyiben ez kisebb, mint az előző minimum - illetve az első összehasonlítás előtt beállított kellően nagy szám -, a range blokk x, z koordinátáit, fényességi eltolását és a rajta végrehajtott transzformáció kódját eltároljuk. A belső ciklus végén a legjobban hasonlító blokk adatait tárolják a változók, amelyeket a könnyű kezelhetőség végett struktúrába foglalunk (affinmap). Ezt a struktúrát mentjük le a kimeneti állományba.A külső ciklus leforgása után a tömörítés végéhez értünk, a file a kép helyreállításához szükséges összes információt tartalmazza. A tömörített állomány mérete csak a betömörítendő kép dimenzióitól függ. Minden affin transzformációs blokk 7 bájtot foglal, a kép méretei 4 bájton írhatóak le. Ez alapján a következő képlet körülbelül megadja a file méretét:
![]()
Azért kell körülbeliségről beszélnünk, mert az átlapolódások miatt egy teljes sorral vagy oszloppal nőhet a hossz. Ha a fenti képlettel számolunk, akkor egy tömörítetlen képpel szemben 50 %-os arány érhető el. Azonban ha megvizsgáljuk a kimeneti állományunkat, jól láthatjuk, hogy azon például egy huffman tömörítést elvégezve még jobb, akár nagyságrendekkel is eltérő eredményt érhetünk
el.A betömörítés a range blokkok osztályozása vagy más keresési algoritmusok alkalmazása nélkül túl lassú, átlagos személyi számítógépen nem igazán várható ki. Az általam készített program egy Pentium® 100 MHz-es számítógépen egy 160x100-as dimenziójú kép tömörítését 8 perc alatt végezte el.
A kitömörítést a decompress
függvény végzi, amely az állományok megnyitása után beolvassa a kép méreteit tartalmazó első két adatot. Ezt követően a kimeneti állományba helyezi a TGA fejlécet. A tömörített file teljes méretéből meghatározzuk az affintérkép struktúrák számát:![]()
A range illetve domain blokkok száma természetesen ugyanennyi lesz. A transzformációs térképstruktúrák (affinemap
) számára egybefüggő memóriaterületet foglalunk le, amelyre az affinelist fog mutatni. Az adatok beolvasása után a bemeneti file már le is zárható.A tömörítéshez hasonlóan elkészítünk egy-egy range és zsugorított range blokk struktúrát, illetve helyet foglalunk egy teljes és egy leátlagolt képnek. Ezt követően a képterületet pontjait 128-as értékkel töltjük fel. Ez az érték az intenzitásskála közepén helyezkedik el, ezért átlagos intenzitású képeknél várhatóan a legkevesebb idő alatt eléri a megfelelő értéket.
Most értünk a ciklusokhoz. A külső ciklus az iterációk megfelelő számát biztosítja. Ez a szám a felhasználó által definált. Az első művelet, amelyet elvégzünk, az a kép leátlagolása, amivel egyben az elméleti range blokk buffer területére másoljuk a képet. A
mapptr mutató itt kapja meg alapértékként az első affintérkép struktúra címét.A belső ciklus sorban végighalad a teljes kép összes domain blokkján, mindegyikhez megkresve a térkép által hozzárendelt zsugorított range blokkot. A zsugorított range blokkot a leátlagolt képterületről vesszük ki. Először az intenzitását toljuk el a megfelelő mértékben, majd végrehajtjuk
rajta a kívánt transzformációt. Az ezek után létrejött blokkot másoljuk a teljes kép területére. A mapptr mutatót megnöveljük, ami típusa miatt a következő affintérkép struktúrára fog mutatni.A ciklusok befejeztével, a teljes kép területen rendelkezésre
álló – feltehetően – az eredeti képtől nem sokban különböző blokkot a kimeneti állományba mentjük. A kitömörítési idő lényegesen – nagyságrendekkel - rövidebb, mint a betömörítésre szánt. Nem sokkal marad el egy JPEG állomány kitömörítési idejétől, tehát olyan helyeken is fel lehet használni, ahol az időtényező meglehetősen fontos.
6.4 A tömörített file felépítése
A tömörített file első két integer típusú változója a kép méreteit tartalmazza. Ezek után sorban az affintérkép struktúrák következnek, amelyek az 3. tábla szerinti felépítésűek. A tömörített file elrendezése tehát az 4. tábla szerinti.
|
Változó |
Típus |
Méret bájtokban |
Funkció |
|
range_x |
unsigned short |
2 |
A range blokk vízszintes koordinátája |
|
range_y |
unsigned short |
2 |
A range blokk függőleges koord inátája |
|
shift |
Short |
2 |
Az intenzitás eltolásának értéke |
|
Transtype |
Char |
1 |
A végrehajtandó transzformáció kódja |
3. tábla: Az affintérkép struktúra elemei
|
Vízszintes felbontás |
Függőleges felbontás |
Affintérkép struktúra I. |
Affintérkép struktúra II. |
… |
Affintérkép struktúra N. |
4. tábla: A tömörített file felépítése
Mivel a program TGA formátumot képes konvertálni, erről is szükséges egy rövid ismertető. A
tga.h header állományban definált struktúraelemek a következő leíró adatoknak felelnek meg.|
Tga_hdr struktúra |
Típus |
Hossz |
Funkció |
|
ID |
Unsigned char |
1 |
Az ID mező hossza |
|
CMAPTYPE |
Unsigned char |
1 |
A színtérkép típusa |
|
IMPTYPE |
Unsigned char |
1 |
A kép típusa |
|
COL1 |
Short |
2 |
A színtérkép első el emének mutatója |
|
COL3 |
Short |
2 |
A színtérkép hossza |
|
COL5 |
Unsigned char |
1 |
A színtérkép mérete |
|
XORIGIN |
Short |
2 |
A kép vízszintes poziciója |
|
YORIGIN |
Short |
2 |
A kép függőleges poziciója |
|
WIDTH |
Short |
2 |
A kép vízszintes mérete |
|
HEIGHT |
Short |
2 |
A kép függőleges mére te |
|
DEPTH |
Unsigned char |
1 |
Színmélység |
|
DESCRIPTION |
Unsigned char |
1 |
Képleíró bitek |
5. tábla: TGA fejléc
A fenti adatokból felismerés szempontjából DEPTH a legfontosabb, mert ennek 3-as értéke jelenti azt, hogy szürkeárnyalatú képpe
l állunk szemben. A program természetesen a WIDTH és a HEIGHT mezőket is használja.6.6 Ötletek a program továbbfejlesztésére
Néhány módon még kényelmesebbé illetve hatékonyabbá tehető a program. Részletekbe való mélyedés nélkül az alábbi módosítási ötletetek vetődnek fel:
A szoftver telepítésében az InstallShield Express van segítségünkre. A telepítő könyvtárból a SETUP.EXE-t kell elindítani, ami a telepítési folyamatot automatikusan vezérli. A feltelepített program ezután a startmenüből, vagy a
compfrac.exe állománnyal indítható.A képernyőn indítás után egy ablak jelenik meg, amelynek
file menüje egyértelmű utasításokat tartalmaz. A compress menüpontot választva tömöríthetjük össze a 8 bit szürkeárnyalatú képet. Először az ezt tartalmazó állományt kell kiválasztanunk az előugró dialógus segítségével, majd a létrehozni kívánt file megnevezése jön. Ennek ajánlott .CIF kiterjesztésűnek lennie, amit a program fel is ajánl. A két file kiválasztása után kezdődik a tömörítés folyamata. Ennek százalékos állapotáról folyamatos információt szolgáltat egy megjelenő státuszablak. Előfordulhat, hogy a program nem válaszol a tömörítés ideje alatt, de amíg a státuszablakban változást látunk, a szoftver megfelelően működik.A kitömörítés hasonló módon zajlik, amelyet a file menü decompress
pontjának választásával indíthatunk. Először a tömörített CIF állományt majd a kitömörítés célpontját képző új file nevét kell meghatároznunk. A kitömörítés folyamatáról nem kapunk információt, mivel az meglehetősen rövid, azonban a művelet végén az eredményről értesít minket a program.Az options
menüpont választásával előugró dialógusablakban állíthatjuk be a kitömörítéskor elvégzendő iterációk számát. Minél magasabb ez az érték, annál szebb, az eredetihez hű képet kapunk. Az iterációk száma függ a kép méretétől is, nagyobb képhez érdemesebb nagyobb értéket választani. Az alapbeállítás 16, ami közelítőleg 200x200-as felbontás igényeinek általában megfelel.A programot az exit menüpont választásával hagyhatjuk el. A help menü about
pontjában pedig információt kaphatunk a szoftverről.A szakdolgozatom témája a fraktálok és alkalmazásaik voltak. A munka elején ismertettem a tipikus és gyakran előforduló fraktálok matematikai alapjait. Ez után bemutattam két rendszert, amelyek a fraktálok leírására alkalmasak. A következő fejezetben ismertettem néhány alkalmazási területen betöltött szerepüket, úgy mint művészetek, kép- és hangfeldolgozás, szociológia és gazdaság. Ezt a képek tömörítésén
él alkalmazott fraktáltechnológia leírása követte az 5. fejezetben. Ezeket a szabályokat alkalmazva készítettem egy, a fraktáltömörítést szemléltető programot, amely 256 szürkeárnyalatú képek tömrítésére alkalmas.The fractals and their applications were introduced in my professional work. At the beginning I explained mathematical forms of typical and frequently appearing fractals. Then I introduced two systems, what are for describing fractals. After that I presented the role of fractals in some application areas, including art, image and sound processing, sociology and economics. The terms of image compression using fractal technology was introduced in the 5th part. Using these terms, a demo program was built by me, to show an example of fractal compression. This program is capable of compressing 256 level grayscale images.
Interneten elérhető oldalak: